56

ПОСТРОЕНИЕ ГЕОМЕТРИЧЕСКИХ ФИГУР КАК СРЕДСТВО РАЗВИТИЯ МЫШЛЕНИЯ ШКОЛЬНИКОВ

К.В. ВОСКАНЯН

В традиционной дидактике до сих пор процесс обучения геометрии начинается не с практических действий по созданию геометрических объектов, не с задач по построению простых фигур, а с анализа готовых чертежей. При этом задачи на построение простых фигур вводятся в учебный процесс не как источник возникновения геометрических понятий, а как вспомогательный учебный материал, способствующий якобы развитию логического мышления школьников, которые не понимают, почему при построении простых фигур надо выполнять именно то, а не другое действие, указанное в учебниках, откуда взялись эти действия и зачем, какую цель преследует их выполнение. Остается нераскрытым и процесс образования геометрических объектов. Способ доказательства теорем излагается как самостоятельная теоретическая деятельность, не связанная с практическим способом образования фигур и существующая как бы вне их.

Пути образования чертежа и понятий специально не изучались. Поэтому и нет разъяснений, как можно изготовить предметы, имеющие формы геометрических фигур, как воспроизвести результаты действий в материализованной форме. Школьники рисуют геометрические фигуры, а не строят их. При таком рисовании не выявляются генетические действия, являющиеся основой образования фигур, не сохраняются размеры исходных элементов целостной фигуры. Поэтому этот процесс в учебной деятельности школьников выступает, скорее всего, как неосмысленный. Построение простой геометрической фигуры с заранее известными величинами их элементов — это особая задача и она в корне отличается от эмпирического рисования фигур.

Определения геометрических понятий, а также словесная формулировка теорем и задач генетически связаны со способами построения чертежа. В процессе обучения дело обстоит иначе — сначала дается словесная формулировка теорем и задач, на основе которой школьники пишут условие задачи и строят чертеж, поэтому в процессе решения задач и доказательства теорем главным средством полагается словесное содержание. Однако это не значит, что словесная формулировка и условия содержат в себе больше информации, чем чертеж.

В древности перед земледельцами не раз вставала проблема восстановления прежней формы участков земли, границы которых исчезали после разлива рек. Для восстановления полей при разливе рек и вычисления их площадей древние землемеры и математики выполняли и практические действия, позволяющие при необходимости изобразить форму любого земельного участка. Воспроизведение результатов практических действий в материализованной форме привело к образованию геометрического чертежа как модели. Поэтому генезис образования геометрических понятий надо искать внутри геометрических задач на построение, при таком подходе чертеж выступает в функции модели.

При исследовании чертежа как модели ученые выявляли новые свойства геометрических объектов, на основе которых формулировались разнообразные теоремы и задачи. В процессе обучения математике в целом важно не только обнаружить материальную основу соответствующего понятия посредством «особой» формы предметной деятельности, но и следить за процессом видоизменения понятий, выявляя одновременно те способы учебно-познавательной деятельности, с помощью которых школьники могут усвоить математические понятия. Поэтому формирование теоретического мышления школьника в области математики связано

с моделированием геометрических соотношений на основе построения разнообразных чертежей, которые обеспечивают осознание школьниками самих этих соотношений в общетеоретической форме.

По выражению Н.М. Бескина [1], при построении чертежей должны сохраняться два основных требования: наглядность и удобоизмеримость. При наглядности изображение чертежа должно быть похоже на оригинал, а при удобоизмеримости должны сохраняться все масштабные размеры оригинала. В традиционной дидактике и педагогической психологии фактически построение чертежа рассматривается соответственно требованиям наглядности, без учета удобоизмеримости. Поэтому при построении чертежей школьники не следят за правилами, а обычно копируют образцы — «чертеж в учебнике и чертеж учителя на доске».

С целью более обстоятельного рассмотрения и разъяснения поставленных вопросов, в 1972—1982 гг. в двух классах — VI и VII школ № 33, 79 Еревана — курс геометрии преподавался нами на основе практического и схематического моделирования геометрических соотношений [3]. Исходные математические понятия вводились в форме учебных задач, решение которых требовало выполнения «особой» формы предметных действий. При помощи дидактических средств (планок с отверстиями, разноцветных ниток, проводов, иголки, картона и т.д.) школьники изготавливали предметы с данными величинами их элементов, имеющих форму геометрических фигур. Затем результаты этих действий воспроизводились посредством различных моделей. Содержание понятий устанавливалось ими не сразу, а через осуществление разных видов конструктивной деятельности. Фактически школьники практически изготавливали предметы, имеющие форму треугольника, четырехугольника и т.д., после чего строили сами геометрические фигуры как особые модели.

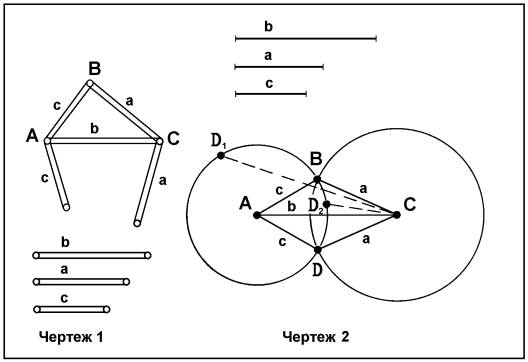
Приведем пример усвоения понятия «треугольник». Школьники должны были с помощью трех планок а, б, с с отверстиями на концах изготовить предмет в форме треугольника. Сначала они поставили одну планку б (см. чертеж 1), затем соединили и укрепили ее один конец с концом второй планки с, после чего один конец другой планки а соединили и укрепили со свободным концом планки б, и посредством вращения укрепили два свободных конца планок а и с друг с другом. Так образовался предмет, имеющий форму треугольника. Школьники увидели, что вершина В изготовленного треугольника АСВ образовалась при вращении планок а и с вокруг прикрепленных точек А и С. Эти практические действия по нашей просьбе школьники повторили несколько раз с целью усвоения того, что в основе изготовления и построения треугольника лежат действия, связанные с описанием окружности.

На следующем этапе школьники повторили способ построения фигуры треугольника в материализованной форме. При этом вместо планок использовались отрезки, величины которых были равны величинам планки. Материализованные действия построения геометрических объектов выступили основой их моделирования. Однако не все школьники при воспроизведении результатов практических действий изобразили треугольник, сохранив при этом размеры сторон. Данный факт говорит о том, что школьники, видимо, еще не осознавали, что в основе построения фигуры треугольника лежат действия, связанные фактически с построением соответствующей окружности, где сторона треугольника является ее радиусом. Перерисованный треугольник не мог удовлетворить требованию задачи. Если после нескольких попыток практического изготовления треугольника школьники не могли интериоризировать результаты своих действий, им предлагалось вложить в свободные концы отверстий планок а и с сердцевину карандаша и изготовить треугольник. Здесь они замечали, что в результате движения планок на бумаге описывались две взаимопересекающиеся окружности. Соединив точки их пересечения с точками

А и С, получились треугольники АВС и ADC (чертеж 2). Таким образом, усваивался способ построения треугольника и воспроизводились его результаты на основе соответствующей знаковой модели.

Используя планки произвольной величины, школьники убедились, что изготовить треугольник возможно не всегда. В результате этих практических действий и моделирования они самостоятельно пришли к выводу, что треугольник нельзя изготовить, и, следовательно, построить его модель, если: а) сумма двух его сторон равна третьей стороне; б) сумма двух его сторон меньше третьей стороны, т.е. треугольник можно построить при условии, что сумма двух его сторон больше третьей стороны. После того как способ построения треугольника по данным величинам трех его сторон был усвоен школьниками, им было предложено построить два треугольника с одинаковыми данными на картоне, вырезать их и наложить друг на друга. Здесь школьники практически убедились, что треугольники совпадают тогда и только тогда, когда соответствующие их элементы совпадают. Тем самым они смогли самостоятельно придти к выводу, что треугольники называются равными, если у них соответствующие стороны и соответствующие углы равны, т.е. Δ АВС равен Δ А1В1С1, если АВ=А1В1; AC=A1C1; ВC=В1C1; ∟АВ=∟А1В1; ∟AC =∟A1C1; ∟ВC=∟В1C1.

На основе чертежа 2 школьники теоретически доказали, что если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.

Для доказательства этого положения чертеж 2 сгибается по лучу АС. При этом вершина D Δ ADC совпадала с вершиной В Δ АВС. Школьники допускали, что вершина D не совпадает с вершиной В, а занимает положение D1 на окружности А (с). Однако по построению точка D должна лежать одновременно и на окружности С (а). Из чертежа видно, что D1C >CD, а также D1C >BC. Таким образом, доказывалось, что при этом точка D1 не может

лежать на окружности С (а). Если предполагалось, что точка D занимает положение D2, тогда АD2=АD=АВ=с, а из чертежа видно, что СD2<ВС и СD2<СD. По условию это тоже невозможно. Оставалось принять, что при сгибании чертежа по лучу АС точка D совпадает с точкой В. Это значит, что Δ ADC совпадает с Δ АВС. Следовательно, Δ ABC= Δ ADC.

При подобном построении треугольника на основе одних и тех же действий возникает представление не только о равенстве треугольников, но и много новых понятий: четырехугольник, биссектриса угла, высота треугольника, две взаимно расположенные окружности и связанные с ними понятия. Так, рассматривая равенство треугольников АВС и ADC, школьники приходили к выводу, что ∟ВАC=∟DAC. А это значит, что луч или отрезок АС делит ∟BAD пополам. Тут же давалось определение понятию «биссектриса угла». Чертеж 2 давал возможность сформулировать различные задачи на доказательство и на построение. Так, школьникам предлагалась задача: «Построить угол, равный углу данного треугольника». Затем, после того как требование задачи было выполнено, учитель предлагал: «Построить угол, равный изображенному углу АВС». Он хотел проверить, осознают ли школьники, что построение единичного угла влечет за собой построение целостного треугольника. Учитель читает задачу вслух: «Построить угол, равный изображенному на доске углу АВС. В нашем распоряжении только планки с отверстиями разных размеров, линейки, но нет транспортира и циркуля. Постройте и докажите, что построенный угол равен данному».

Ученик. Можно рассматривать этот угол как внутренний угол замкнутого треугольника?

Учитель. Да.

Ученик. В таком случае я с помощью линейки соединю точки В и С и получу нужный мне треугольник. Затем построю треугольник, равный этому треугольнику. А если треугольники равны, то будут равны и их соответственные углы.

Учитель. Верно.

Ученик. Можно использовать тот же способ, что был использован и при построении равнобедренного и равностороннего треугольников: с помощью двух равных планок изготовить равнобедренный треугольник и на его основе построить чертеж.

Учитель. Но данный угол не является углом равнобедренного или равностороннего треугольника, он дан изолированно.

Ученик. Нужно отложить на сторонах данного угла от вершины В равные отрезки ВА и ВС. Точки А и С соединить друг с другом. Получится равнобедренный треугольник, две стороны которого известны. Величину же третьей стороны можно измерить и построить треугольник, равный Δ АВС. Если треугольники равны, то равны и их стороны и углы.

Учитель. Правильно, можно построить и таким способом. В обоих случаях в основе построения изолированного угла лежит способ построения целостного треугольника, т.е. построение одной фигуры влечет за собой построение другой фигуры. В частности, построение угла логически вытекало из способа построения треугольника.

Из рассуждений школьников видно, что в их мышлении четко проявляется диалектика общего и отдельного. Примером этого является специфическое содержание отдельного понятия внутри развивающегося целого, объективная связь отдельного и целого. Способ построения отдельного угла превращается в способ построения целостного треугольника. Построение угла, равного данному, выступает как необходимое следствие способа построения треугольника, как целостной замкнутой фигуры. Принципиально важным было и то, что все эти понятия были сформированы в системе. Школьники владели способами переходов от одних понятий к другим. Таким образом, практический способ изготовления треугольника и его модельное воспроизведение ведет к тому, что школьники усваивают целостный способ построения треугольника как вообще.

Все это говорит о том, что в геометрии

непосредственным предметом мышления является идеализированный образ фигуры. Мысленная трансформация возможна только на основе обобщенного способа построения модели (чертежа) геометрического объекта. На основе реального построения чертежа, как особого вида учебно-познавательных действий, происходит полноценная идеализация геометрического объекта. С помощью обобщенного, способа школьники в уме могут воссоздать другой идеальный образ, опираясь на то же умственное действие.

Проведенные со школьниками эксперименты позволяют предположить, что характерной особенностью геометрических чертежей является: 1) чертеж демонстрирует реально те обстоятельства, которые приводят к формированию той или иной теоремы и задачи, 2) на основе чертежа выявляются переходы исходных понятий в производные, 3) чертеж выступает в роли своеобразной модели, построение которой требует воспроизведения предметных действий, позволяющих обнаружить содержательные связи и отношения между разными понятиями в составе общего геометрического понятия, 4) чертеж является источником различных проблемных ситуаций, которые в дальнейшем, как скрытые задачи, оформляются в словесно-абстрактную форму, которую школьник должен определить самостоятельно в процессе решения; 5) на основе чертежа воссоздаются знаковые модели тех проблемных ситуаций, которые выступают в опосредствованной форме; 6) чертеж является своеобразным мостиком между «предметными» и умственными действиями, т.е. выступает в роли среднего звена между чувственной и рациональной ступенями познания и обеспечивает последовательные переходы между практической и теоретической деятельностью.

Мыслительный процесс школьников формируется и протекает эффективно, если они видят за понятием его предметно-деятельностный источник. При этом они опираются именно на понятие, а не на слова. Только в таком случае мышление школьников будет носить теоретический характер.

При осуществлении анализа математических объектов необходимо учитывать отношение всех частей целого и их специфические особенности, так как все отдельно выделенные элементы логически поддерживают друг друга. При теоретическом анализе надо исходить из требования теорем и задач, так как не все элементы и понятия внутри сложного чертежа занимают равное по своей значимости место. Исходя из этого, необходимо расчленять чертеж и выделять фигуры, имеющие между собой содержательные связи.

Эксперимент показал, что сущность теоретического мышления заключается не в том, чтобы словесно фиксировать полученные сведения о вещах, а раскрывать логическое и психологическое содержание научных знаний. Сущность такого мышления заключается в построении и воспроизведении системы математических понятий, благодаря чему раскрываются особенности и функции собственно теоретических понятий и их взаимосвязи в составе целостной системы.

Экспериментальное обучение показало, что фактически на основе одного и того же практического действия можно построить целый ряд геометрических фигур, внутри которых каждое единичное понятие не только отражает определенные стороны, но и взаимосвязи внутри целого, поэтому знания школьников приобретают системный характер. Вместо оперирования совокупностью единичных понятий (при традиционном обучении) у школьников экспериментальных классов формируются целостные системы знаний. В результате действий с геометрическими объектами школьники открывали теоретическое содержание возникающих понятий.

В процессе построения геометрических объектов школьники выявляли и обобщали результаты действий, лежащие в основе образования понятий. При этом они переходили от предмета к открытию связей и соотношений между его элементами посредством понятий и, наоборот, от понятий к предметным действиям. В учебной деятельности школьников обнаруживались взаимодействия

и взаимопереходы различных видов мышления, благодаря чему школьники в своих рассуждениях часто включали понятийное значение образов и знаков, исследовали образные и знаковые модели, выявляли частные формы их проявления. На основе чертежа они самостоятельно формулировали словесное содержание задач на доказательство и осуществляли действия по построению соответствующих объектов. Экспериментальное обучения показало, что выявление скрытых свойств и мысленное воспроизведение процесса создания геометрических фигур возможно лишь при сформированности общего способа их построения.

Итак, в деятельности по усвоению геометрических понятий важное место должно отводиться способу построения чертежей, которые выступают как содержательные модели соответствующих геометрических объектов. Опираясь на эти модели, школьники получают возможность выявлять такие особенности усваиваемых понятий, которые не отражены в словесных определениях.

Только самостоятельно изготавливая предмет и воспроизводя схематически результаты соответствующих действий, можно построить теоретическое представление об объекте, и тогда чертеж в учебной деятельности школьника может выступать в функции модели, а процесс построения чертежей — как особый вид учебно-познавательной деятельности.

1. Бескин Н. М. Изображение пространственных фигур. М., 1971. 80 с.

2. Богоявленский Д. Н., Менчинская Н. А. Психология усвоения знаний в школе. М., 1959. 347 с.

3. Давыдов В. В. Виды обобщения в обучении (логико-психологические проблемы построения учебных предметов). М., 1972. 422 с.

4. Кабанова-Меллер Е. Н. Психология формирования знаний и навыков у школьников. Проблема приема в умственной деятельности. М., 1962. 376 с.

5. Применение знаний в учебной практике школьников / Под ред. Н.А. Менчинской. М., 1961. 375 с.

Поступила в редакцию 6.VI 1988 г.